更前面的知识:树的概念
先来说说前面的芝士:
- 路径长度 从根结点到目标结点经过的结点数量(边的数量)。
- 权值 一个结点的权值可以是人为赋予的一个数。
- 结点的带权路径长度 从根节点到当前结点的路径长度乘结点的权值。
- 树的带权路径长度 整个树中叶子结点的带权路径长度总和。
哈夫曼树是二叉树,且哈夫曼树的带权路径长度最小,哈夫曼编码会用到。
哈夫曼树的构建
前面写了,哈夫曼树的带权路径长度最小,若想带权路径最小,则权值小的结点的路径长,权值大的结点路径短。哈夫曼树构建的结点都必须是叶子结点,例如用 1 2 5 6 构建的哈夫曼树是这样的: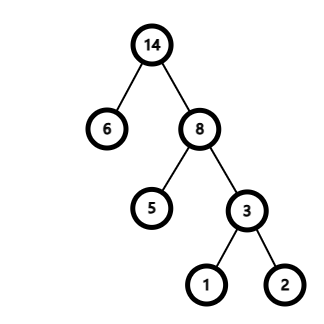
这个树的带权路径长度为 25。
构造过程:
- 选出权值两个最小的结点合并;
- 将两个点从将要合并的结点序列中删除,加入两个结点的和;
- 重复以上步骤,直至达到要求。
演示: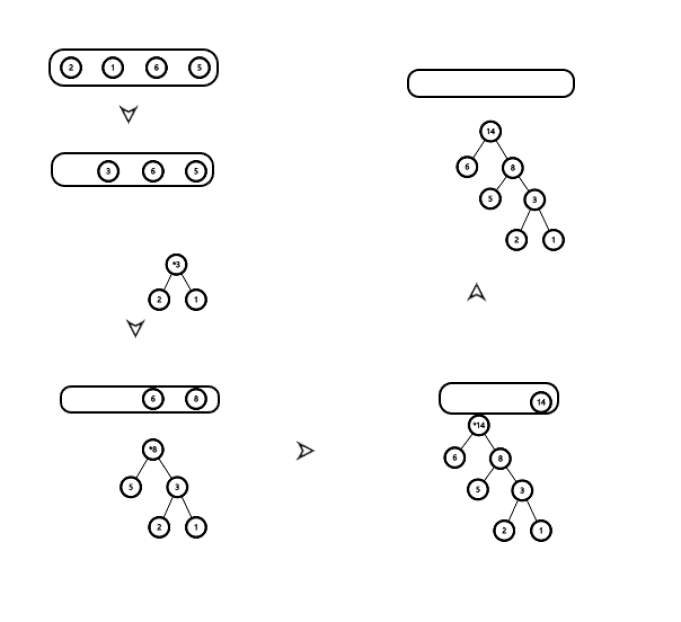
哈夫曼编码
基于哈夫曼树,按照字符出现的频率(也就是哈夫曼树中的权值)进行二进制编码。
也就是用哈夫曼树对一串字符进行编码,可以认为左子树是 0,右子树是 1。(说不清楚啊)
哈夫曼编码是贪心的思想,为了使信息量最小化,可以用到哈夫曼树。