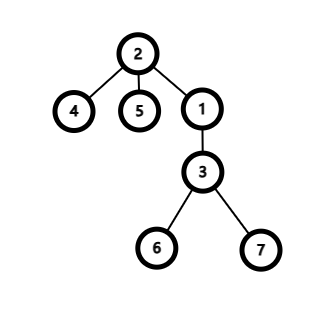
树也是一种数据结构，它是非线性数据结构，它能很好地描述一个数据集合中的分支和层次，是一个比较重要的课题，以后的搜索和竞赛都有可能要用到它。树形结构的应用非常广泛，什么索引、语法结构。虽说概念比较繁琐 老师讲了一个小时。有点让人头疼（我咕了好多篇笔记了）。

树的概念

前面

前置芝士，简单说一下这些奇怪的名称：

• 树中的每一个元素称为结点 node。
• 两个结点之间的线称为边 edge。
• 通过几条边，这几条边组成路径。

树的结点一般画为圆圈，树若画出来也就是几个结点（圆）和几条边（线）组成的图，比较形象化，实际的树的储存方式是通过链表中的数据域将一个个结点（元素）连接起来，比较麻烦，后面再说。
还有一个概念：树的边的个数比树的结点的个数少一。也就是说，假设树的结点的个数为 $n$，则树的边的个数为 $n-1$。

判断一张图是否为树

树最重要的就是每两个结点之间有且只有一条路径可以到达，也就是说，不可以形成环，不可以在一个树中无法到达所有结点。例如，下面就是一个树：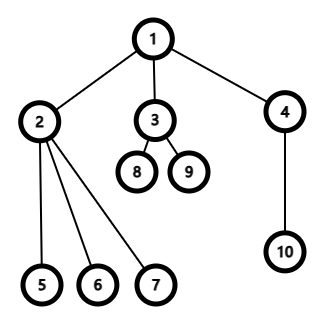

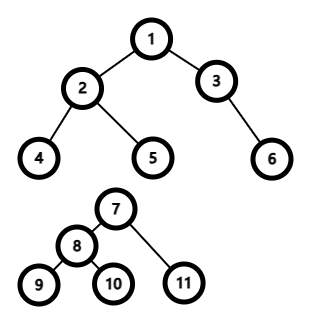
下面两张图不是树，他们分别违反了“不可以形成环”、“不可以在一个树中无法到达所有结点”。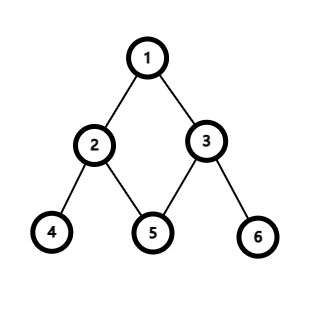

更多的概念

首先放一张图：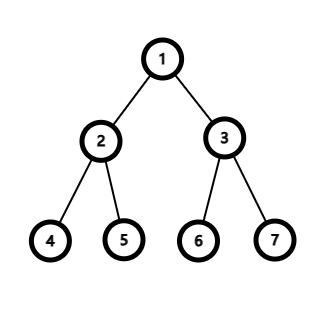

以这张图为例，来说下面的概念吧。
根结点 root：根结点通常在最上方，是所有子结点的父结点。在上面的那张图中，结点 1 就是整张图的根结点。在上面的图中，根结点可以更换，也不会影响到什么，但是根结点一变就会让树形态发生变化（假如结点 2 是整个树的根结点，那么树会变下面的图）。一个树是必须要有根结点的，根结点只有一个。
父结点 parent（双亲结点） 子结点 child（孩子结点）：一个结点的分支就是那个结点的子结点，相反那个结点是分支结点的父结点。子结点通过父结点到达。例如结点 4 5 是结点 2 的子结点，结点 3 是结点 6 7 的父结点。
兄弟结点：同一个父结点的子结点称为兄弟结点。例如结点 4 5 互为兄弟结点，6 7 互为兄弟结点。
度：树的度就是一个结点子结点的个数。例如结点 2 的度就是 2，因为它只有两个子结点。
深度：从根结点到当前结点的层数，根结点的深度是 1。例如，结点 1 深度为 1，结点 2 3 深度为 2，结点 4 5 6 7 深度为 3。
叶子结点：一个结点的度为 0，就叫做叶子结点。例如结点 4 5 6 7 都是叶子结点。
n 叉树：在树中，这个数是多少叉看度最多的结点，例如这个树就是二叉树（也比较特殊，后面讲）。
子树：假设将树中任意一个度不为 0 的结点与它的父结点切断它们之间的边，那么断开的那一部分又能成为一个新的树，称为子树。例如结点 2 4 5 可以组成一个子树。

还有一大堆子子孙孙祖先的什么的，懒得写了。说真的，感觉说多了意义不大。

二叉树的概念

n 叉树中，又出现了一个二叉树 Binary Tree 这么个奇怪的概念。什么左子树右孩子什么的不记了，就讲三个我认为比较重要的。

完美二叉树：
也叫做满二叉树。简单来说就是一个深度为 $n$ 的二叉树，拥有 $2^n - 1$ 个结点。看着的话就是若再增加一个结点使其继续为二叉树，深度就必须要加一了。刚才的示例图就是一个完美二叉树。
完全二叉树：
完全二叉树的叶子结点可以不是满的，但是剩下的叶子结点必须都在图的左边。例如那张示例图若将结点 7 去掉，它就只是一个完全二叉树。
完满二叉树：
完满二叉树的结点除了叶子结点以外其他结点的度都必须是 2。示例图若将结点 4 5 去掉，它就只是一个完满二叉树。

树的储存

一大堆基础概念，已经够呛了（悲）。学到树的储存已经开始逐渐迷惑。。。
一般来说，树也是不太可能用真正的指针链表来储存，毕竟太难写了，内存限制一般比时间限制够用一些，就用数组模拟链表。链表就是要关心指针域，下面就是一大堆奇奇怪怪的方法。

可能用不到的

父亲表示法：顾名思义，指针域指向父结点。
孩子表示法：指针域指向子结点。
父亲孩子表示法：双向链表结构，也没啥用。

可能会用到的

孩子兄弟表示法：适用于二叉树，也是一个双链表结构，一个结点连接其子结点和兄弟结点。
邻接矩阵表示法：见这里。
邻接表表示法：也看上面。

假设根结点为 2 时的情况：