原本像在别的文章的基础上再加的,但是还是新建了一个文章。主要就是讲一下昨天老师讲过的东西。
对于二叉树和其他树什么的,可以再看看“树”这个标签里的几篇文章。这里主要讲的都是二叉树的性质。
定义
二叉树得符合树的特点,同时树上度最大的结点不得超过 2。即:
- 树的特点
- 无向联通图,没有环
- 有 $n$ 个结点,$n - 1$ 条边
- 二叉树的类型
- 空树
- 当有结点时,结点应最多只有 $2$ 个子树
另一个说法就是:一棵不为空的树,其根结点的度不大于 $2$,且它的左子树和右子树也都为二叉树的树(这是递归的说法)。
几种类型
这里只说之前没有记过的类型,之前两(三)种类型看这篇。
二叉搜索树
二叉树上的任意一个结点,其左子树上的所有数(权值)都小于它,右子树上的所有数(权值)都大于它。就是按照中序遍历(看这篇)该二叉搜索树,得到的(权值)数列是有序的。
同二叉树的定义(递归说法)一样,二叉搜索树的左子树和右子树都是二叉搜索树。二叉搜索树的基本操作最优时间复杂度为 $O(\log n)$,最差为 $O(n)$($n$ 为结点数)。但目前还没有学二叉搜索树的应用。
例如,下面的图片就是一个二叉搜索树(csAcademy graph editor 炸了,只能用 mermaid 生成的图片凑合):
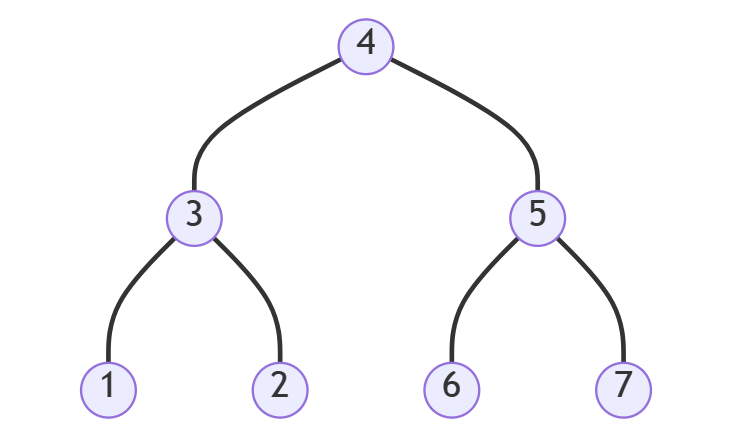
平衡二叉树
这里以平衡树中的 AVL 树来说。它的左子树的深度和右子树的深度的差不大于 $1$。例如完全二叉树就是衡二叉树。
平衡二叉树的主要用途就是减小时间复杂度,不会像链一样遍历速度很慢。当一棵理想的平衡二叉树的节点数为 $n$ 时,遍历的时间复杂度应为 $O(\log n)$。
性质
- 结点数量
- 一棵深度为 $i$ 的二叉树最多(即完美(满)二叉树)有 $2^i - 1$ 个结点。
- 因为二叉树的深度为 $j$ 的一层最多有 $2^{j - 1}$ 个结点。
- 叶子节点数为 $x$ 的二叉树,则它度数为二的结点个数为 $x - 1$
- 对于完全二叉树
- 具有 $n$ 个叶子结点的完全二叉树的深度为 $\lfloor \log_2 n \rfloor + 1$
- 若对有 $n$ 个结点的完全二叉树按层从上到下,从左到右依次编号为 $1, 2, …, n - 1, n$,对于任意结点编号为 $i$ 则:
- 若 $2 \times i > n$ 则它是叶子结点,否则其左节点编号为 $2 \times i$,(当 $2 \times i < n$ 时)右结点编号为 $2 \times i + 1$
- 当 $i \ne 1$(非根结点)其双亲结点编号为 $\lfloor i \div 2 \rfloor$
做例子的图:
这是一个完美(满)二叉树,也是完全二叉树。
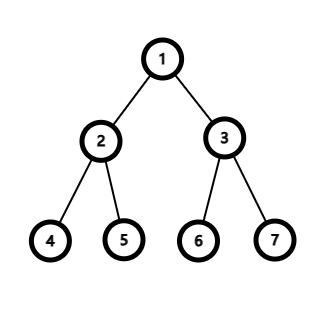
可以发现其结点符合上面的规则。
存储和遍历
可以去看看这个题单,以及“二叉树的前序、中序、后序遍历”的代码部分,里面有关于遍历的信息。
开头也说过,这篇文章并没有追加到“二叉树的前序、中序、后序遍历”这篇文章上是因为新建一篇文章比较醒目。