二叉树的前序遍历中序遍历和后序遍历是比较重要的CCF办的比赛要考（雾。可以通过这三个遍历的顺序结果确定整个树的结构。前序遍历是根左右，中序遍历是左根右，后序遍历是左右根。（不想多写什么了）

前、中、后序遍历代码

此代码对于输入格式：

• n: 有 n 个结点
• 接下来 n 行，第 i 行：每行两个整数 a, b，a 是 i 结点左子树的根的编号，b 是 i 结点右子树的根的编号。
• a, b 为 -1 时表示为空。

整合起来的代码：

#include <cstdio>
using namespace std;

struct node
{
    int l, r; // l: 左子树的根的序号，r: 右子树的根的序号
};

int n;
const int TEMP = 1e5 + 3;
node tree[TEMP];
bool flag[TEMP];

/*
void dfs(int x) // 前序：根左右
{
    printf("%d ", x); // 先找根结点
    if(tree[x].l != -1) dfs(tree[x].l); // 判断是因为如果子树为空就不用遍历了（同下），再找左结点
    if(tree[x].r != -1) dfs(tree[x].r); // 最后找右结点
}
void dfs(int x) // 中序：左根右
{
    if(tree[x].l != -1) dfs(tree[x].l); // 先找左结点
    printf("%d ", x); // 再找根（父）结点
    if(tree[x].r != -1) dfs(tree[x].r); // 最后找右结点
}
*/
void dfs(int x) // 后序：左右根
{
    if(tree[x].l != -1) dfs(tree[x].l); // 先找左结点
    if(tree[x].r != -1) dfs(tree[x].r); // 再找右结点
    printf("%d ", x); // 最后找根（父）结点
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        tree[i].l = a;
        tree[i].r = b;
        if(a != -1) flag[a] = 1; // --> 说明该结点是某个结点的子结点，打标记，一定不是根结点
        if(b != -1) flag[b] = 1; // ----^ 为找根结点准备
    }
    
    int root;
    for(int i = 1; i <= n; i++)
    {
        if(flag[i] != 1) // 不是任何结点的子结点，没有父结点
        {
            root = i; // 就是根结点
            break;
        }
    }
    dfs(root); // 所有的遍历都要从根结点开始
    
    return 0;
}

例题：洛谷[P1305] 新二叉树 就是前序遍历，只是和上面代码的输入格式不太一样。

实践：前序遍历中序遍历确定树

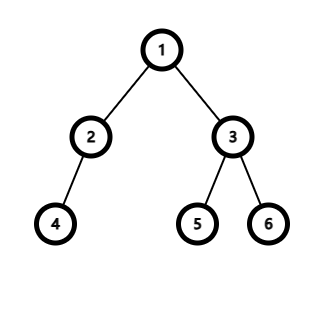
前序遍历：1 2 4 3 5 6
中序遍历：4 2 1 5 3 6

先来看前序，由于前序遍历的顺序是根左右，那么 1 一定是整个树的根结点。随后在中序遍历找到 1，即可判断这个二叉树的左子树和右子树，就是这样分开来：
前序遍历：1 2 4 3 5 6
中序遍历：4 2 1 5 3 6
在继续分下去，得到：
前序遍历：1 2 4 3 5 6
中序遍历：4 2 1 5 3 6

最终，得到这样一个树：