写递归的要点
明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节， 否则就会陷入无穷的细节无法自拔，人脑能压几个栈啊。
—— OI-wiki

递归，就是一个函数自身调用自身。递归起到类似与循环的效果。但是，与循环不同，递归可以分支。如果循环一定是一条直线，那么递归可能是树形结构。

循环 -> 递归

前面说了，循环和递归很像。那么，我们可以将 for 循环尝试转为递归。先来一个循环的示例：

for(int i = 1; i <= n; i++)
{
    printf("qwq, %d\n", n);
}

首先，让我们来想一想，for 循环的括号中 3 个语句分别是干什么的呢？

1. int i = 1; 这是循环的初始化，定义了一个变量 $i$，将其赋值为 $1$。
2. i <= n; 这是循环每次进行下去的条件，当 $i>n$ 时即退出循环。
3. i++ 这是循环每次结束后干的事，当执行完循环体时， $i$ 则加 $1$。

这样回忆下来，可以发现，在 for 循环的括号中 3 个语句其实可以拆分出来。如下：

int i = 1; // int i = 1;
for( ; ; )
{
    if(i > n) break; // i <= n;
    printf("qwq, %d\n", n);
    i++ ; // i++
}

那么，直接将 for( ; ; ) 改一下就好了吧？就像这样子：

int i = 1;
void rcsn()
{
    if(i > n) break;
    printf("qwq, %d\n", n);
    i++ ;
}

等等，只将 for( ; ; ) 改为 void rcsn() 似乎不太对，少了什么语句，函数不会自动循环（递归）啊。还有，函数哪儿来的 break;？
是的，递归，就是要自己调用自己。函数的结束，是该使用 return。应该这样修改：

  int i = 1;
  void rcsn()
  {
-     if(i > n) break;
+     if(i > n) return;
      printf("qwq, %d\n", n);
      i++ ;
+     rcsn();
  }

好了，这样就可以完整地运行了：

#include <stdio.h>

int n;
int i = 1;
void rcsn()
{
    if(i > n) return;
    printf("qwq, %d\n", n);
    i++ ;
    rcsn();
}

int main()
{
    scanf("%d", &n);
    rcsn();
}

递归的分步思想

前面说了，递归是可以分支的。那么，它其实比循环方便的多。就比如说，输入一个整数 $n$，按照字典序输出 $1 \sim n$ 数字不重复的排列。$1 \le n \le 9$。

总不可能用 if 一个一个判断，然后来一个“循环 $n$ 嵌套”吧。而递归是可分支的。可以创建一个递归函数，在递归中使用 for 循环确定递归次数。用一个数组记录是否重复。代码如下：

#include <iostream>
using namespace std;

int n;
bool flag[12];
int a[15];

void dg(int id)
{
    if(id > n)
    {
        for(int i = 1; i <= n; i++)
        {
            cout << "    " << a[i];
        }
        cout << endl;
        return;
    }
    
    for(int i = 1; i <= n; i++)
    {
        if(flag[i]) continue;
        
        flag[i] = 1;
        a[id] = i;
        dg(id + 1);
        flag[i] = 0;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin >> n;
    dg(1);
    
    return 0;
}

但是，递归并不是刚完成就返回，而是完成了整个分支才返回。以 $n=3$ 为例，画个上面那个递归函数的图：

（说明：圆圈中的数字是前进的顺序，从小到大；实线箭头和虚线箭头先走实线，走完以后再走虚线；箭头上的数字代表输出的值。

递归的分治思想

分治，就是将一个问题分解为多个问题，然后再进行解决。用咱们老师的一个词概括，就是：

分而治之

举个例子：一件工程做 100 个零件，接活的找了 10 个人帮忙，那 10 个人又去找了 10 个人，每一组的 10 个人做完了向上头汇报，上头 10 个人又向接活的人汇报。
这其实就是一个递归分治的过程，这么一个例子体现了分治的基本步骤：

1. 分解：“接活的找了 10 个人帮忙，那 10 个人又去找了 10 个人” -> 将原问题分解成子问题
2. 解决：“每一组的 10 个人做完了” -> 子问题独立求解
3. 合并：“（10 个人做完了）向上头汇报，上头 10 个人又向接活的人汇报。” -> 将子问题合并为原问题

当分解到指定条件时，就开始解决——通常是直接返回特定的数据。

题目举例：CodeForces 1829D
这道题目要分解为两个任务，第一是总金币数的三分之一，第二是总金币数的三分之二。分解停止开始解决的的条件有三个，分别是 $x==m$（符合条件），$x<m$（不符合条件），$x % 3 \ne 0$（不符合条件）。
可以这样想：若符合条件返回 $1$，不符合返回 $0$，将返回结果相加。若最终结果大于零，输出 YES，否则输出 NO。
代码如下：

#include <cstdio>
using namespace std;

int n, m;
int t;

int dg(int x)
{   
    if(x == m) return 1;
    if(x < m || x % 3 != 0) return 0;
    
    
    int ans1 = dg(x / 3);
    int ans2 = dg(x / 3 * 2);
    // printf("ans1:%d, ans2:%d\n", ans1, ans2);
    
    return ans1 + ans2;
}

int main()
{
    scanf("%d", &t);
    
    for(int i = 1; i <= t; i++)
    {
        scanf("%d %d", &n, &m);
        
        int ans = dg(n);
        // printf("ans:%d\n", ans);
        if(ans > 0) printf("YES\n");
        else printf("NO\n");
    }
    
    return 0;
}

剪枝

题外话：感觉和递归有关的分类都一团乱了，感觉 DFS 原本应该放在同一篇文章里的，剪枝和分治也应该独立说一篇。

简短的概述：
可以说，递归也就是暴力。暴力有两个代名词：枚举、递归。同枚举差不多，递归也有优化的方案，那就是剪枝。剪枝，顾名思义，就是把不需要的分支剪掉，把不可能的选项排除，在递归中，可以大大提升运行速度。

题目举例：
洛谷 P1219
这道题目是 DFS 中比较经典的八皇后问题。在每行、每列、每个对角线上都只能有一个棋子（皇后）。那么，以下剪枝的几点可以确定：

• 当这一行放过以后，就开始放下一行，将这一行排除。
• 当这一列放过以后，就将这一列打上标记，不再将棋子放在这一列。
• 这一个对角线放过后，打上标记，不再将棋子放到对角线上

但是，对角线的标记比较难弄，对角线似乎无法打标记。对角线的标记并不是无解，对角线的 (x,y) 是有规律的。引用原文图片来找规律。
先看右斜的对角线有什么规律：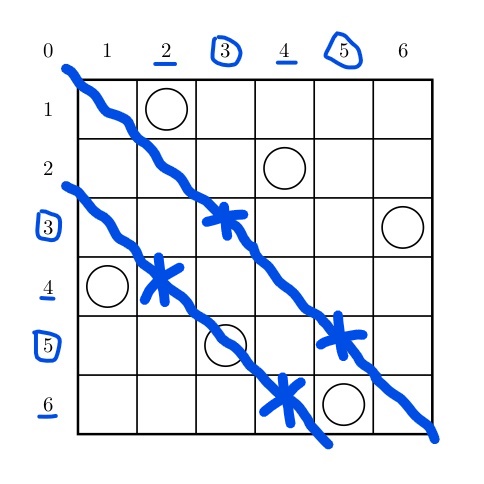

可以看到，中间一条蓝色的线对应圈起来的坐标，(3,3) (5,5)；靠左一条蓝色的线对应划线的坐标，(4,2) (6,4)。不难看出，$3-3=0=5-5=0; \hspace{5px} 4-2=2=6-4=2$。可见，同一条右斜对角线上，x 坐标减 y 坐标的绝对值相等。但是相对的对角线上x 坐标减 y 坐标的绝对值也一样，这就比较麻烦。C++ 不能用负数，也不能两条对角线都是同一个标记。老师给了我们一个办法，将他们的差加上 20（别的数也行），问题就解决了。
再看左斜的对角线有什么规律：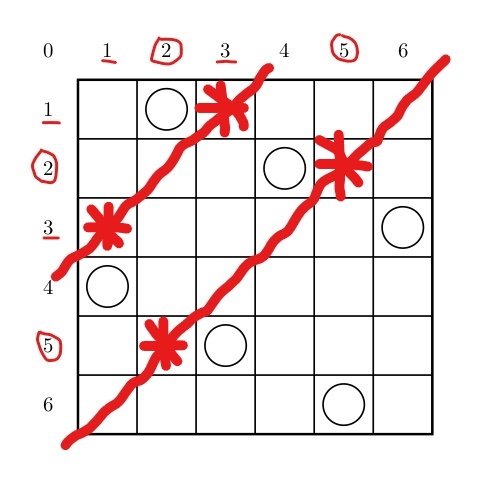

同上，中间一条对应 (2,5) (5,2)，左上一条对应 (1,3) (3,1)。与右斜的对角线不同，它们不是差有规律而是和有规律。$2+5=7=5+2=7; \hspace{5px} 1+3=4=3+1=4$。那么，打标记时将 x+y 作为下标即可。

加上深搜，代码就出来了：

#include <cstdio>
using namespace std;

bool flagy[50], flagzx[50], flagyx[50];
int sum = 0;
int n;
int s[50];

void dfs(int x)
{
	if(x == n + 1)
	{
		sum++ ;
		if(sum <= 3)
		{
			for(int i = 1; i <= n; i++)
			{
				printf("%d ", s[i]);
			}
			printf("\n");
		}
		return;
	}
	
	for(int i = 1; i <= n; i++)
	{
		if(flagy[i] == 0 && flagzx[x + i] == 0 && flagyx[x - i + 20] == 0)
		{
			flagy[i] = 1;
			flagzx[x + i] = 1;
			flagyx[x - i + 20] = 1;
			s[x] = i;
			dfs(x + 1);
			flagy[i] = 0;
			flagzx[x + i] = 0;
			flagyx[x - i + 20] = 0;
		}
	}
}

int main()
{
	scanf("%d", &n);
	
	dfs(1);
	printf("%d\n", sum);

	return 0;
}